学术咨询服务正当时学报期刊咨询网是专业的学术咨询服务平台!
发布时间:2015-03-18 09:46所属平台:学报论文发表咨询网浏览: 次
论文摘要:传统的聚类算法在处理复杂特征数据时效果不理想,为此提出使用高斯径向基核函数将原空间上的数据映射到高维特征空间后,再用蚂蚁算法进行第一次聚类,针对第一次聚类结果得到较多簇等问题,提出再用马赛克算法进行二次聚类,得到较为接近真实情况
论文摘要:传统的聚类算法在处理复杂特征数据时效果不理想,为此提出使用高斯径向基核函数将原空间上的数据映射到高维特征空间后,再用蚂蚁算法进行第一次聚类,针对第一次聚类结果得到较多簇等问题,提出再用马赛克算法进行二次聚类,得到较为接近真实情况的簇数目。UCI数据集中的鸢尾花数据集,第三类数据由于与其它两类有特征交叉现象,很难被传统聚类算法准确识别,但本文的核空间二次蚂蚁聚类算法在此数据集上取得较为理想的结果。
论文关键词:数学论文发表,核函数,蚁群聚类,马赛克算法
(一)引言
聚类(clustering)分析已经广泛地用于许多应用领域。Deneubourg[2]等于1991年,根据蚂蚁堆积尸体的行为提出了基于蚂蚁的聚类基本模型(DM),首次将蚁群算法应用于聚类分析。随后,Ramos等人提出了ACLUSTER算法[3]。ACLUSTER算法改进了以往蚂蚁聚类模型中蚂蚁的拾起和放下物体的策略,并且引入信息素模型指向人工蚂蚁的移动,避免了算法中蚂蚁过多地在无物体分布区域耗时的随机搜索,减少了时间开销;引入了对应于多种任务的响应阈值,使得人工蚂蚁在计算拾起或放下概率时考虑了周围的物体数量,更有利于形成簇;去掉了人工蚂蚁的记忆能力并取消了不同速度的蚂蚁,保持了算法模型的简单性,并减少了相应的计算时间和存储空间开销。这些改进有效地改善了聚类的效果,并能应用于文本聚类、图像模式识别、Web挖掘等任务。
核函数方法能将原空间中的样本映射到未知的高维特征空间,从而优化样本特征,改善学习性能[。本文针对高维数据的特性,将核函数方法引入ACLUSTER蚁群聚类算法,将数据映射到高维特征空间进行聚类,该算法有效地把样本投影成一维的距离数据值,易于聚类。针对ACLUSTER算法收敛速度慢、形成簇过多等问题,本文提出新的聚类策略,通过使用不同参数设置的两次聚类对数据进行聚类。最后通过实验说明,二次快速蚁群聚类算法提高了算法的时间效率,并且改善了聚类的效果。
(二)核空间两点距离的计算方法
在原欧几里德空间中,数据对象X和Y之间的距离定义为:
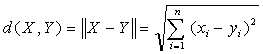
,其中n为对象的维数。
将对象X,Y通过核函数映射到核空间,利用核的定义便可以推导在核空间中的距离。特征空间中的欧几里德距离可表示为:
上式展开得:
因为K(x,y)=φ(x)·φ(y)>,所以将上式直接用核函数表示为:
代入高斯径向基核函数,可推出特征空间中的欧几里德距离:
即为每个物体的核距离值,决定了物体在聚类空间的位置。程序里使用该公式。
参数Y、σ的选择:
(1)Y选坐标原点,容易计算。
(2)
在根号下,因为有平方,X、σ取实数即大于或等于0,但如果σ太大,X变化小,
趋于0,
趋于1,得到的值的变化和1贴得紧;表达式得到的值就分不开,不易区分物体。如果σ太小,
趋于0,同样不易区分物体的核距离值。根据经验,σ取X的中间值即
(j,k是物体编号,i是属性号),即找出离原点最近的物体k,算出最小距离;找出离原点最远的物体j,算出最大距离;最小加上最大两个物体的距离,取一半为σ。
求出每个物体的d(x,y)之后,将物体撒在矩阵上,采用Acluster方法聚类。
(三)核空间二次蚁群聚类算法
Acluster聚类结果得到的簇数量较多,得不到准确结果,这样就需要用二次聚类。收集聚类得到的结果,把它们整理出来,放到小空间聚类,方法采用马赛克算法。
马赛克算法:将这个原25x25的矩阵压缩到13x13矩阵,将大矩阵中划分为2x2一组,每组压缩成新矩阵中1x1的格子,对应地放到新的小矩阵中。规则如下:
(1)如果2x2的格子里没有或者只有一个物体,则新格子里没有物体。
(2)如果有2个物体,则计算随机数,为0则新格子没物体,1则有物体,新物体的核距离值为两个物体的平均值,新标号也为平均值。
(3)如果有3个或4个物体,则新格子里有物体,核距离值和标号都为均值。
核空间二次蚁群聚类算法工作流程图如下:
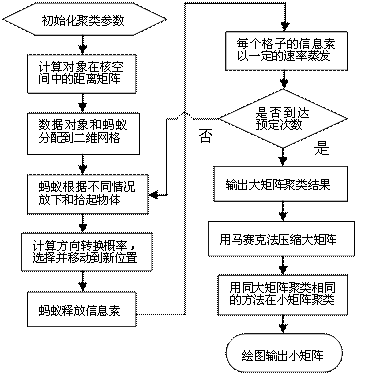
图1核空间二次蚁群聚类算法图
(四)实验结果及分析
实验平台:PC(配置:CPUIntelPentiumDual2.0GHz,内存DDR2G),操作系统为WindowsServer2003EnterpriseEdition。算法使用MSVisualBasic.Net2008编程,数据库采用SQLServer2000实现。
使用UCI数据集中的鸢尾花数据集,该数据集每一行有一朵鸢尾花的萼片长、萼片宽、花瓣长、花瓣宽的数值,一共有150行,分为3种类别:irissetosa(山鸢尾)、irisversicolour(变色鸢尾)、irisvirginica(维吉尼亚鸢尾),每类50行。数据集中的第一、第二类较容易识别,但第三类的特征与第一、第二类有交叉,一般的聚类算法很难准确识别第三类。
实验1:我们使用鸢尾花数据集,使用原空间欧几里德距离值和ACluster算法聚类,聚类参数:蚂蚁数量AntCount=16,最大迭代次数T=10,网格数g=25,k1=0.1,k2=0.3,η=0.07,β=3.5,α=400,γ=0.2。得到了图2示的聚类结果,簇数目很多、较为松散、凌乱,且执行次数再加多,结果离正确值3个簇都是很远。聚类算法的执行结果达不到要求。
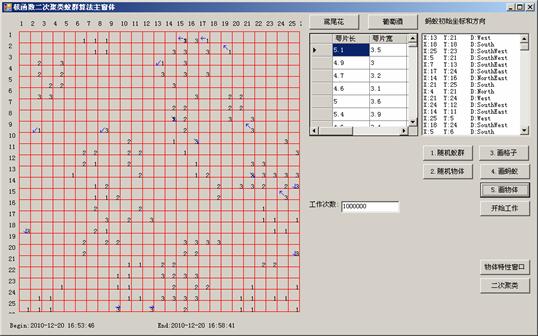
图2欧氏空间聚类结果
实验2:采用本文的核函数二次聚类算法。聚类参数:蚂蚁数量AntCount=16,最大迭代次数T=10,网格数g=25,k1=0.1,k2=0.3,η=0.07,β=3.5,α=400,γ=0.2;核参数
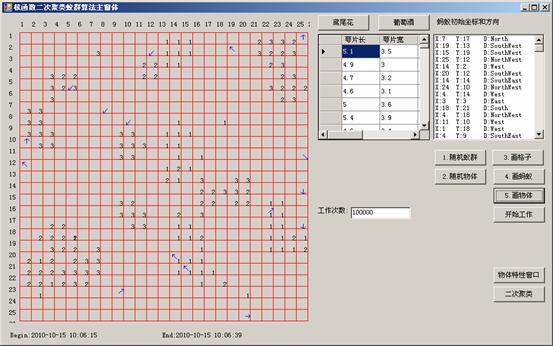
图3核函数第一次聚类结果
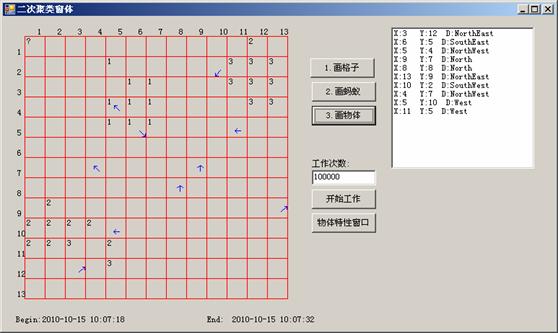
图4第二次聚类结果
在图3中,簇的数目较多,不容易判断出有3簇,但每簇内同类对象较集中。我们采用马赛克法把第一次聚类结果压缩成13x13的矩阵,再进行二次聚类。聚类参数:物体个数ItemNumber=28,蚂蚁数ant=10,网格grid=13,η=0.07,β=3.5,α=400,γ=0.2,k1=0.15,k2=0.35,迭代次数10。图4为第二次聚类结果。我们可以看到数据被聚类成了3大部分,与鸢尾花数据集的3类基本符合。
(五)结论:
核函数二次聚类算法适合于多属性(维)多对象的聚类。将高维数据用核函数映射到一维空间得到核距离值,每个对象对应一个核距离值。将对象撒到平面矩阵中,用ACluster方法使用较小的阈值聚类,在大空间得到规模较小但内部相似度很高的簇,然后将大空间的信息压缩到小空间,再用不同的聚类相关的参数进行第二次聚类,得到较接近真实情况的结果。
参考文献
1 Han J W,Kamber M.数据挖掘:概念与技术[M].北京:机械工业出版社,2008:251-300
2 Deneubourg J L, Goss S, Franks N. The dynamics of collective sorting: robot-like ant and ant-likerobot[C]. Proceedings first conference on simulation of adaptive behavior: fromanimals to animats. Cambridge: MITPress, 1991:356-363.
3 Vitorino Ramos, Fernando Muge, Pedro Pina. Self-Organized Data and Image Retrieval as a Consequence ofInter-Dynamic Synergistic Relationships in Artificial Ant Colonies [C], 2ndInt. Conf. on Hybrid Intelligent Systems, IOS Press, 2002 Vol. 87:500-509.
4 张冰,孔锐,一种支持向量机的组合核函数[J],计算机应用,第27卷第1期,文章编号:1001-9081(2007)01-0044-03
5 徐燕子,覃华.用核空间距离聚类约简大规模SVM训练集[J].微计算机信息, 2010, 15:197-198.
6 http://archive.ics.uci.edu/ml/machine-learning-databases/iris/.
转载请注明来源。原文地址:http://www.xuebaoqk.com/xblw/286.html
《数学论文发表核空间二次蚁群聚类算法的研究_马赛克算法》